KNN & Distance Metrics#
Recap on general concepts#
What’s the difference between supervised and unsupervised learning?#
 Supervised Learning vs. Unsupervised Learning
Supervised Learning vs. Unsupervised Learning
What are the two different tasks that can be solved with supervised learning?#

The KNN Algorithm#
Overview of KNN#
KNN is a supervised learning algorithm
used to solve both regression and classification problems
KNN assumes that similar things exist in close proximity
→ “Birds of a feather flock together”

Why using KNN?#
Despite its simplicity, it was often successful for both classification and regression problems:
handwritten digits
satellite image scenes
it’s good for situations where decision boundary is very irregular
How would you classify the question mark?#

How would you classify the question mark?#

How would you classify the question mark?#

How to measure “close proximity”?#
KNN is based on the idea of “similarity”
mathematically speaking similarity can be calculated via distances
simplest distance would be bee line distance → Euclidean Distance
KNN#
Input:
data with features that are comparable (i.e. can calculate a distance) & target variable
How KNN works:
loop over the observations:
calculate distance to all (brute force) or some (optimized) data points
sort them and pick K “closest”
Output:
Regression: the mean of the neighbors
Classification: the mode of the neighbors
How to train KNN?#
What’s happening when we call knn.fit():
training phase consists of “remembering” / storing all data points
→ training time is very short

How to predict for new instances?#
calculate distance between new observations and every training data point
K closest points are determined
test data are assigned to the class of their K nearest neighbors according to majority voting
→ prediction time can be very high
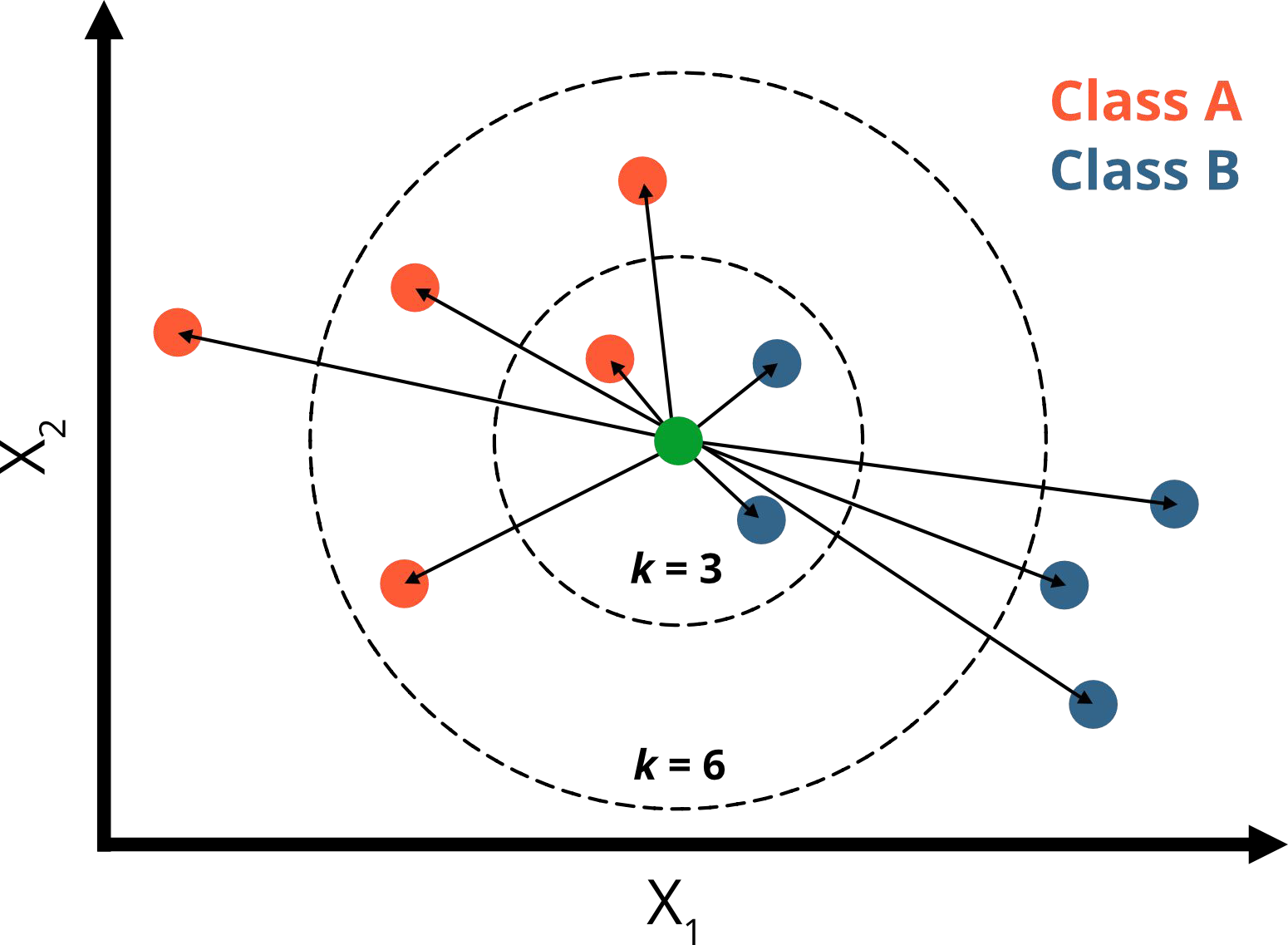
What would you predict for k = 3 and k =6 ?
How to predict for new instances?#
k = 3:
1 neighbor is orange (p=⅓)
2 neighbors are blue (p=⅔)
→ green point belongs to class B
k = 6:
4 neighbors are orange ( p=⅔)
2 neighbors are blue (p=⅓)
→ green point belongs to class A

Notes:
Usually at least one clever student asks what happens in case of a tie.
When there is a tie in k-Nearest Neighbors (KNN) classification, such as when k=3 and there are 3 different classes represented by the nearest neighbors, several tie-breaking methods can be employed. (Uneven k’s only always work for binary classifiction problems).
In binary classification problems use an uneven number for k.
Random selection: One of the tied classes is chosen randomly.
Weighted voting: Instead of simple majority voting, the algorithm can use weighted KNN. In this approach, the distances of the neighbors are considered, giving more weight to closer neighbors.
Reduce k: The value of k can be decreased until the tie is broken. This method always works, as a tie is impossible when k=1.
Prior probability: The class with the higher prior probability (most frequent class overall in the training set) can be selected.
Nearest neighbor: The class of the single nearest neighbor among the tied groups can be used.
Smallest index: The class with the smallest index among tied groups can be chosen.
Include ties: Some implementations allow including all neighbors with distances equal to the kth smallest distance, potentially breaking the tie by considering more neighbors.
What are the assumptions of KNN?#
similar observations belong to the same class / have a similar outcome
no assumption is made on data distribution / mapping function
→ KNN is a non-parametric algorithm
What are some assumptions of linear regression?
Hyperparameters#
What influences the performance of KNN?#
What are hyperparameters of KNN?#
The number of neighbors (K) which is taken to classify.
The distance metric used to determine the nearest neighbors.
The weight applied to neighbours during prediction phase.
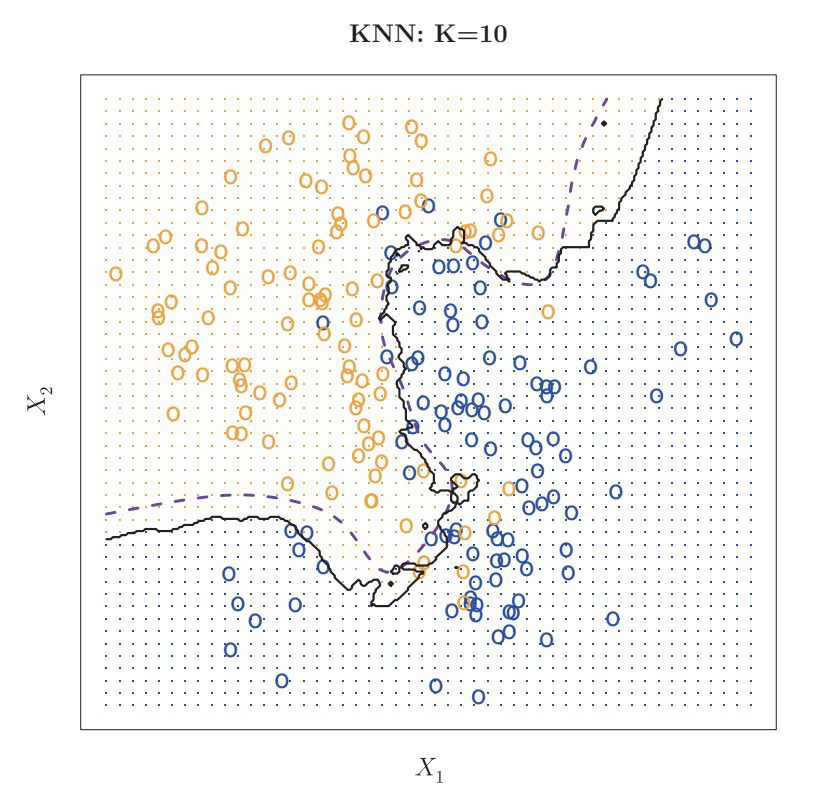
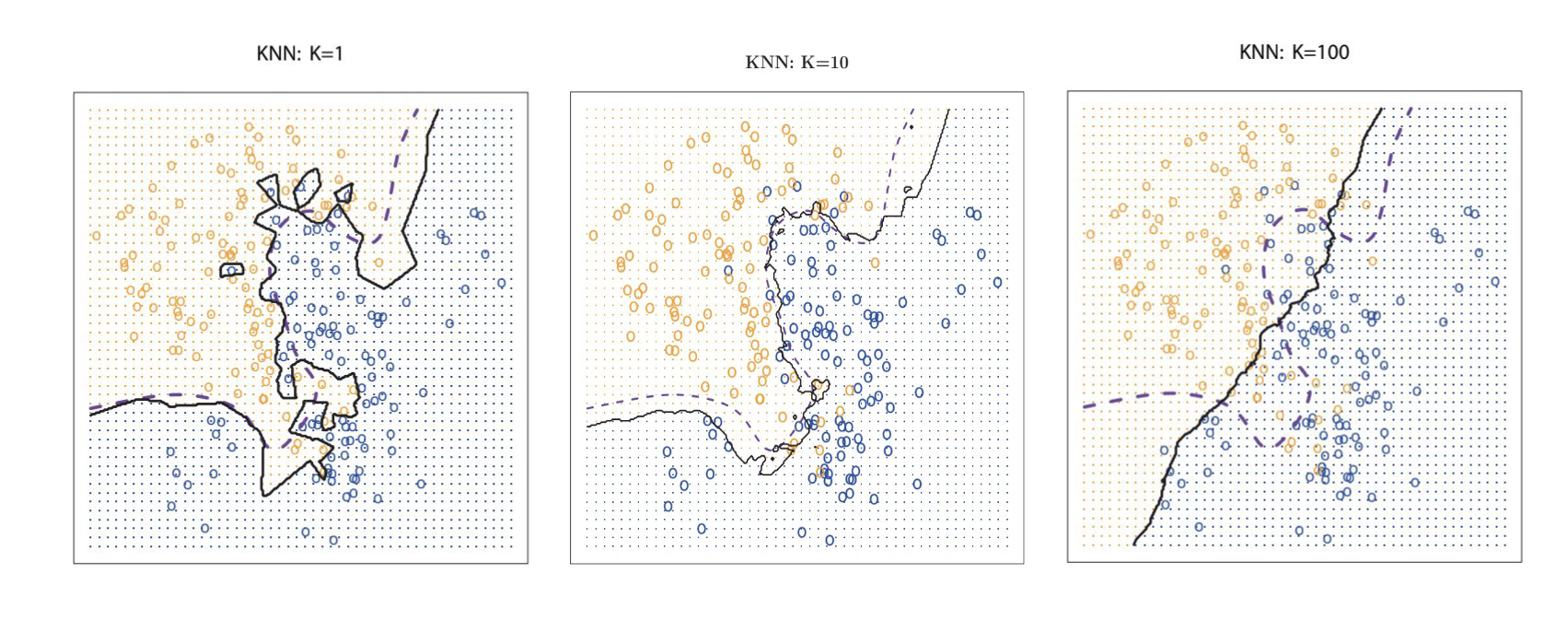
Influence of K#
circles: training data
dashed line: decision boundary of data generating process
solid line: model
grid points: indicating which class is predicted in this area
Influence of K#
How would you interpret these models?
Influence of K#
K=1 → overfitting
K=10 → good fit
K=100 → underfitting

How do we determine the best value for K?#
test different numbers for K (e.g. with GridSearch)
→ take K with lowest error on validation data set

Distance Metrics#
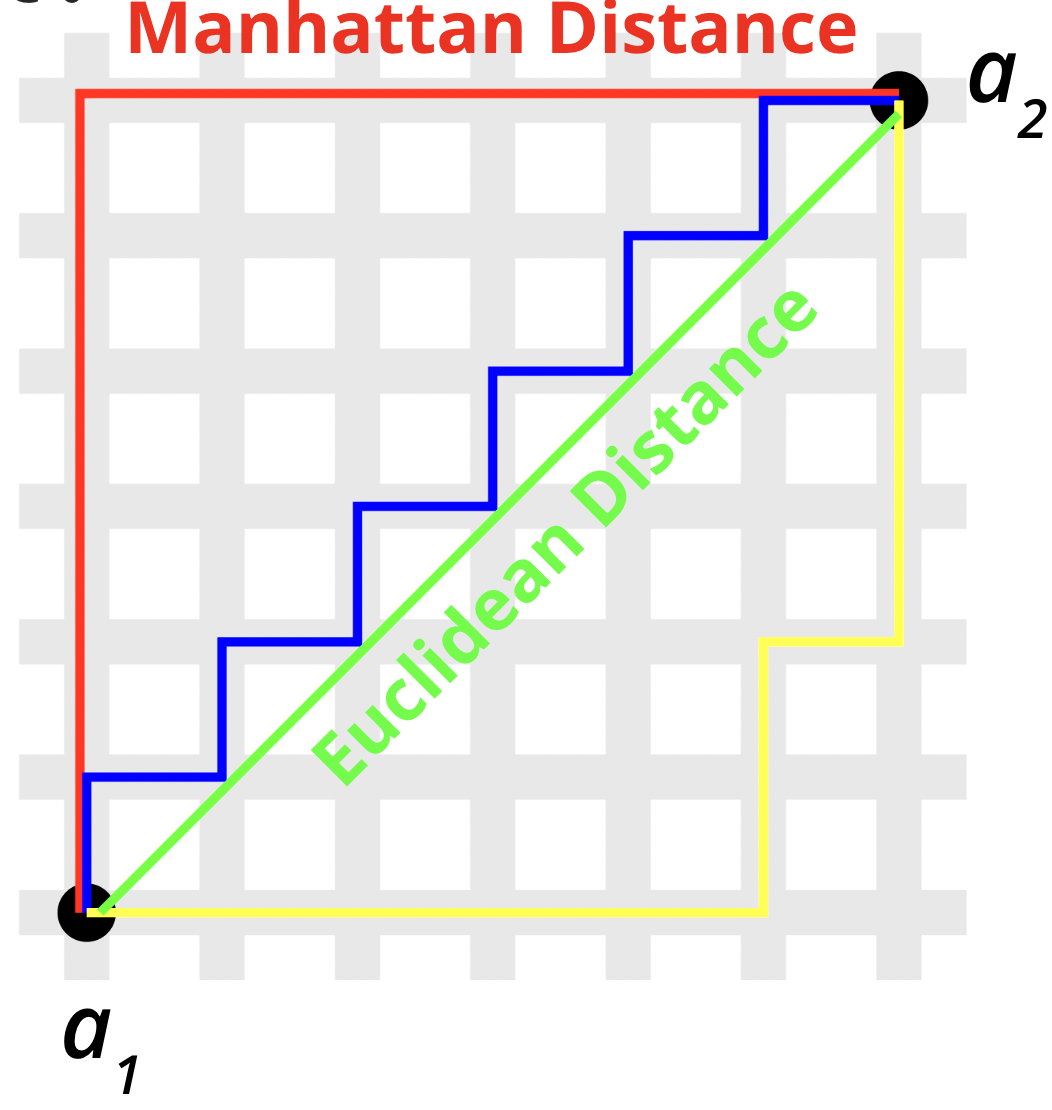
In this example the Euclidean Distance is used.
The Euclidean distance between two points (\(a_1\) and \(a_2\) ) is the length of the path connecting them.
\(\sqrt{\Sigma_{i=1}^{n}(a_{1,i} - a_{2,i})^2}\)

What Distance Metrics exist?#
Euclidean Distance \(\sqrt{\Sigma_{i=1}^{n}(a_{1,i} - a_{2,i})^2}\)
Manhattan Distance \(\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|\)
sum of the absolute differences between the x-coordinates and y-coordinates
(Minkowski Distance \(\sqrt[p]{\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|^p}\))
Minkowski Distance, mostly used cases#
Minkowski Distance: \( \sqrt[p]{\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|^p}\) generalized Distance Metric
Minkowski Distance with p=1: \( \Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|\) Manhattan Distance
Minkowski Distance with p=2: \( \sqrt{\Sigma_{i=1}^{n}(a_{1,i} - a_{2,i})^2}\) Euclidean Distance
Minkowski Distance with p=∞: \( \sqrt[∞]{\Sigma_{i=1}^{n}|a_{1,i} - a_{2,i}|^∞}\) Chebychev Distance
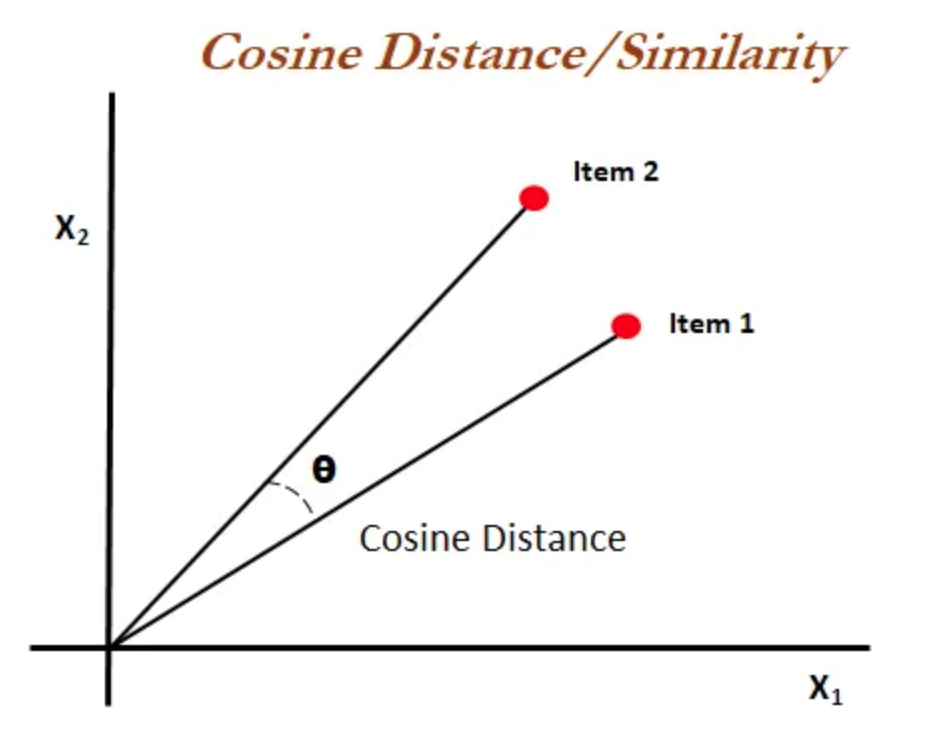
Cosine Distance#
COSINE SIMILARITY: the measure of similarity between two non-zero vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors.
Cosine Similarity: \( S_c(\vec A,\vec B)= cos(\Theta)= { \vec A \cdot \vec B} \div {|\vec A| |\vec B|} \)
COSINE DISTANCE = \( 1 - S_c(\vec A,\vec B) \)